成考数学必背的公式.pdf

成考、全日制大专、专插本、电大、网教咨询请加： daniujiaoyu001 1 斜率公式 2 1 2 1 y y k x x    （ 1 1 1 ( , ) P x y 、 2 2 2 ( , ) P x y ） . 等差数列和公式 Sn=n(a1+an)/2=na1+n(n-1)/2 d 等比数列求和公式 q≠ 1 时 Sn=a1(1-q^n)/(1-q)=(a1-anq)/(1-q) q=1 时 Sn=na1 (a1 为首项 ,an 为第 n 项 ,d 为公差 ,q 为等比 ) 余弦定理 对于任意三角形 ，任何一边的 平方 等于其他两边平方的和减去这两边 与它们夹角的余弦的两倍积，若三边为 a， b， c 三角为 A， B， C ， 正弦定理 R C c B b A a 2 sin sin sin    （ R为 ABC  外接圆半径） 倍角公式 正弦二倍角公式： 0. sin2 α =2cos α sin α 1.Cos2a=Cosa^2-Sina^2=[1-tana^2]/[1+tana^2] 成考、全日制大专、专插本、电大、网教咨询请加： daniujiaoyu001 2 2.Cos2a=1-2Sina^2 3.Cos2a=2Cosa^2-1       sin cos cos sin ) sin(            sin cos cos sin ) sin(            sin sin cos cos ) cos(            sin sin cos cos ) cos(            tan tan 1 tan tan ) tan(            tan tan 1 tan tan ) tan(         2 tan 1 tan 2 2 tan   点到线的距离公式 ： P(x 0,y 0)到直线 Ax+By+C=0 求根公式 平面向量的运算法则。 1） 设 a＝ 11(,)xy ， b＝ 2 2 ( , ) x y ，则 a+b＝ 1212(,)xxyy 。 2） 设 a＝ 11(,)xy ， b＝ 2 2 ( , ) x y ，则 a-b＝ 1212(,)xxyy 。 3） 设点 A 11(,)xy ， B 2 2 ( , ) x y ，则 2 1 2 1 ( , ) AB OB OA x x y y         。 4） 设 a＝ (,),xy R，则 a ＝ ( , ) x y   。 5）设 a＝ 11(,)xy ， b＝ 2 2 ( , ) x y ，则 ab＝ 12 12 ( ) xx yy  。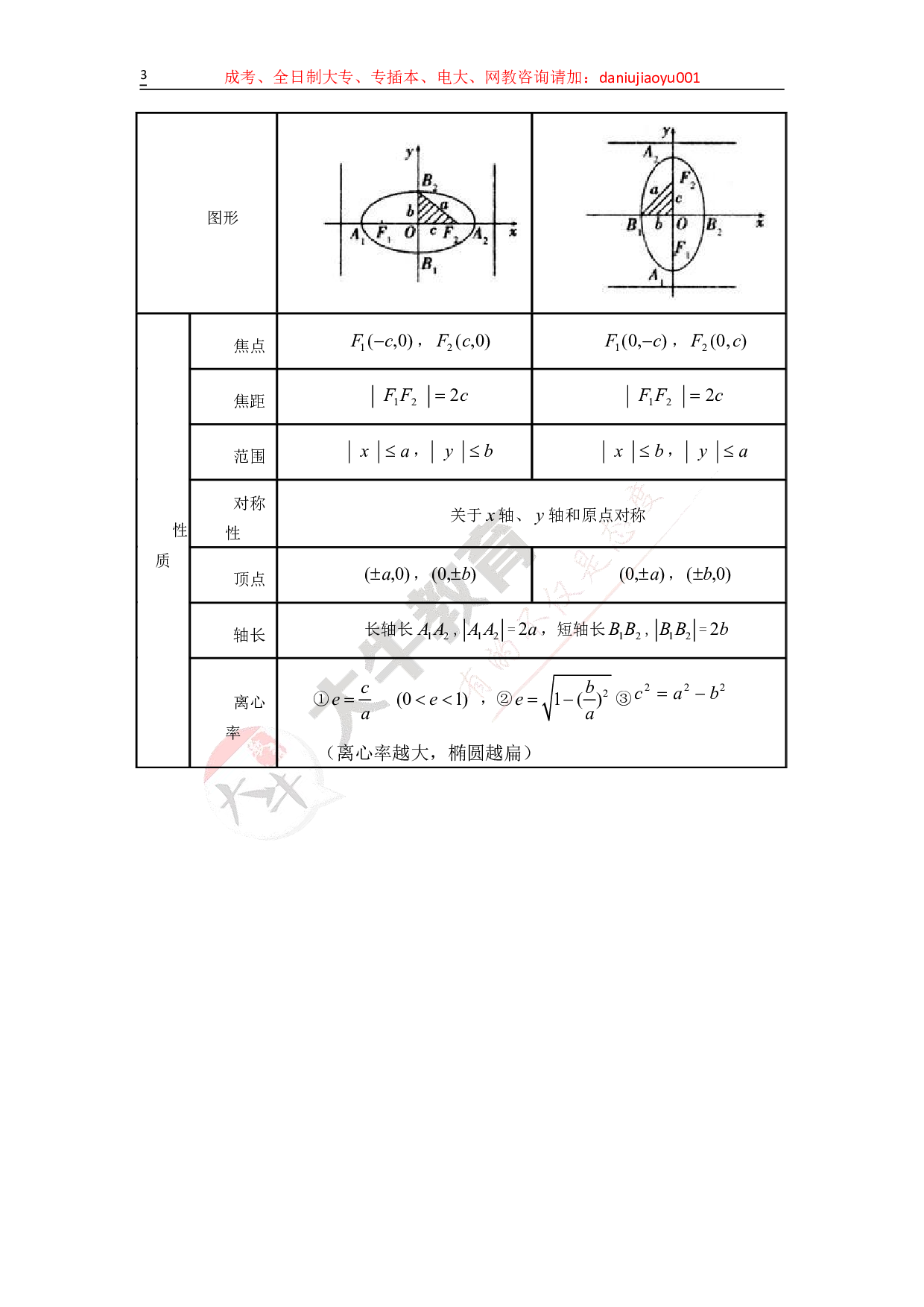 标准方程 1 2 2 2 2   b y a x )0 (  b a 1 2 2 2 2  b x a y )0 (  b a 成考、全日制大专、专插本、电大、网教咨询请加： daniujiaoyu001 3 图形 性 质 焦点 )0, (1 c F  ， )0,(2c F ) ,0(1 c F  ， ),0(2 c F 焦距 c F F 2 2 1  c F F 2 2 1  范围 a x  ， b y  b x  ， a y  对称 性 关于 x轴、 y轴和原点对称 顶点 )0, ( a ， ) ,0( b ) ,0( a ， )0, ( b 轴长 长轴长 1 2 A A , 1 2 A A = a2 ，短轴长 1 2 B B , 1 2 B B = b2 离心 率 ① (01) c ee a  ， ② 2 1 ( )b e a   ③ 2 2 2 b a c   （离