几何手册精编.pdf

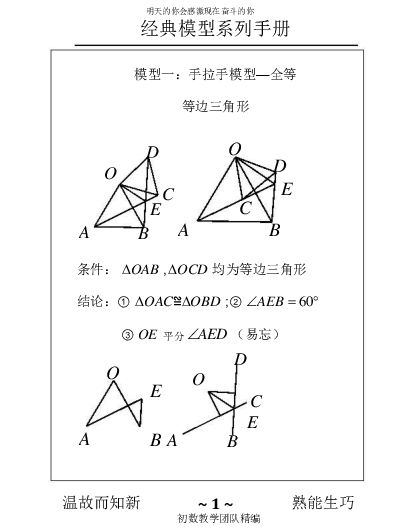
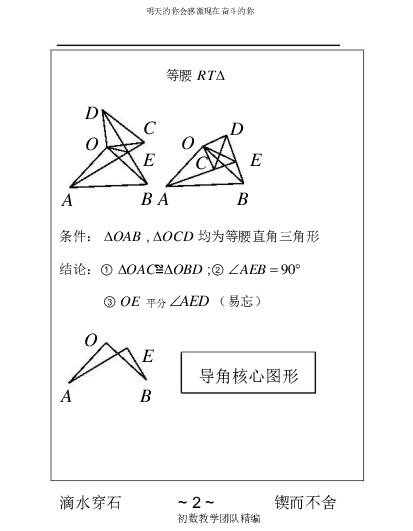
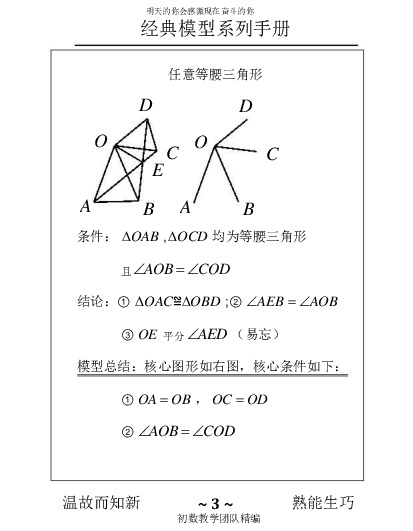
明天的 你会感激现在奋斗的你 初数 教学团队精编 经典模型系列手册 模型一：手拉手模型 —全等 等边三角形 O D D O E C E C A B A B 条件： OAB , OCD 均为等边三角形 结论： ① OAC ≌OBD ;② AEB  60 ③ OE 平分 AED （易忘） D O O E B A C E A B 温故而知新 ~ 1 ~ 熟能生巧 明天的 你会感激现在奋斗的你 初数 教学团队精编 等腰 RT D C E D O O C E A B A B 条件： OAB ,OCD 均为等腰直角三角形 结论： ① OAC ≌OBD ;② AEB  90 ③ OE 平分 AED （易忘） O E 导角核心图形 A B 滴水穿石 ~ 2 ~ 锲而不舍 明天的 你会感激现在奋斗的你 初数 教学团队精编 经典模型系列手册 任意等腰三角形 D D O O C C E A B A B 条件： OAB , OCD 均为等腰三角形 且 AOB  COD 结论： ① OAC ≌OBD ;② AEB  AOB ③ OE 平分 AED （易忘） 模型总结：核心图形如右图，核心条件如下： ① OA  OB ， OC  OD ② AOB  COD 温故而知新 ~ 3 ~ 熟能生巧 明天的 你会感激现在奋斗的你 初数 教学团队精编 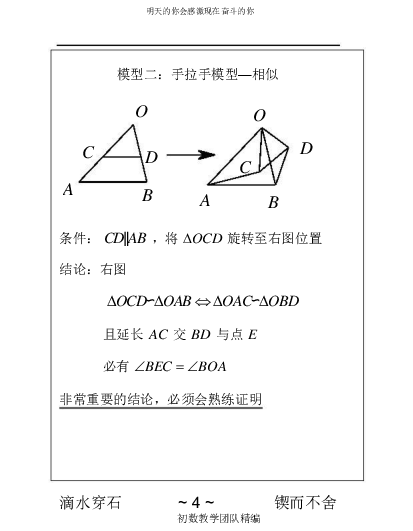模型二：手拉手模型 —相似 O O C D D C A B A B 条件： CD∥AB ，将 OCD 旋转至右图位置 结论：右图 OCD ∽OAB  OAC ∽OBD 且延长 AC 交 BD 与点 E 必有 BEC  BOA 非常重要的结论，必须会熟练证明 滴水穿石 ~ 4 ~ 锲而不舍 明天的 你会感激现在奋斗的你 初数 教学团队精编 经典模型系列手册 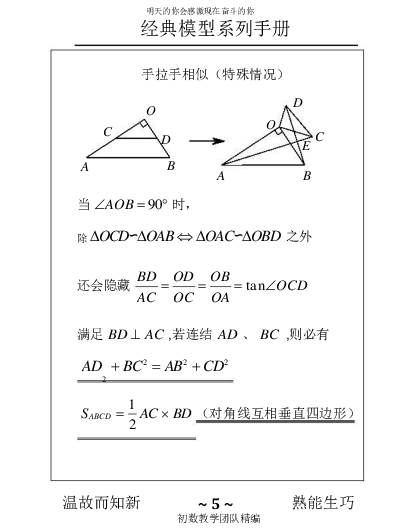手拉手相似（特殊情况） D O O D C C E A B A B 当 AOB  90 时， 除 OCD ∽OAB  OAC ∽OBD 之外 BD OD OB 还会隐藏    ta nOCD AC OC OA 满足 BD  AC ,若连结 AD 、 BC ,则必有 AD 2  BC 2  AB 2  CD 2 1 SABCD  AC  BD （对角线互相垂直四边形） 2 温故而知新 ~ 5 ~ 熟能生巧 明天的 你会感激现在奋斗的你 初数 教学团队精编 模型三：对角互补模型 （全等型 —90°） A A M C E C E D D N O B O B 条件： ① AOB  DCE 90 ② OC 平分 AOB 结论： ① CD  CE ；② OD  OE  2OC 1 ③ SODCE  SOCD  SOCE  OC 2 2 辅助线之一：作垂直，证明 CDM