23 个函数与导函数类型专题
第 1 页
23 个 函 数 与 导 函 数 类 型 专 题
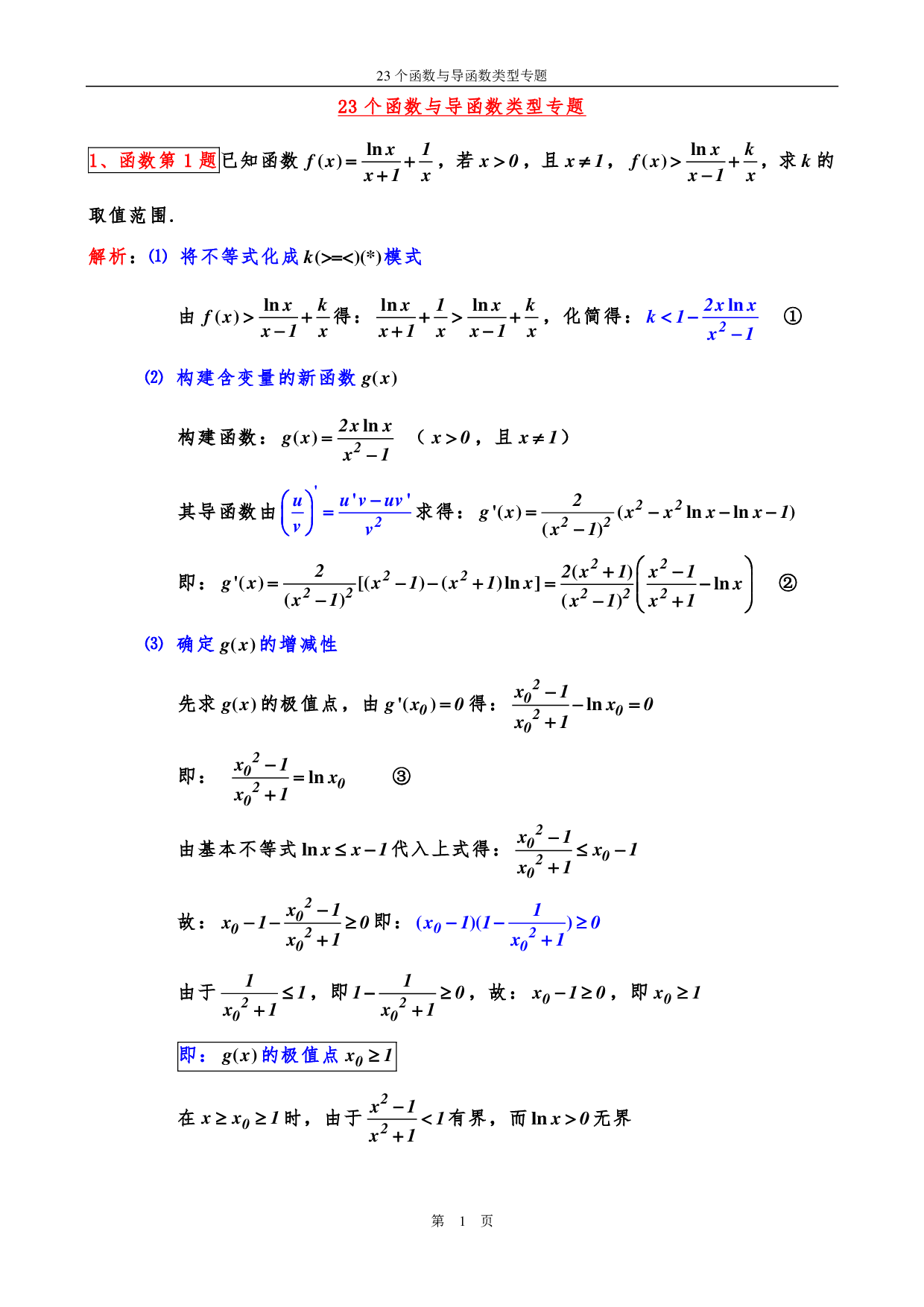
1、 函 数 第 1题 已 知 函 数 , 若 ,且 , ,求 的
取值范围 .
解析 : ⑴ 将 不 等 式 化 成 模式
由 得: , 化简得: ①
⑵ 构 建 含 变 量 的 新 函 数
构建函数: ( ,且 )
其导函数由 求得:
即: ②
⑶ 确定 的增减性
先求 的极值点 ,由 得:
即: ③
由 基 本 不 等 式 代入上式得:
故: 即:
由于 ,即 , 故: ,即
即: 的极值点
在 时,由于 有界,而 无界 ln () x1 fx x 1 x x0 x1 ln () xk fx x 1 x k ( )(*)k ln () xk fx x 1 x ln ln x 1 x k
x 1 x x 1 x ln
2
2 x x k1
x1
()gx ln () 2
2 x x gx
x1
x0 x1 ' ''
2
u u v uv
v v
'( ) ( ln ln )
()
22
22
2 g x x x x x 1
x1
'( ) [( ) ( ) ln ]
()
22
22
2 g x x 1 x 1 x
x1
() ln
()
22
2 2 2
2 x 1 x 1 x
x 1 x 1
()gx ()gx '( ) 0 g x 0 ln
20 0 20
x1 x0
x1
ln
20 0 20
x1 x
x1
ln x x 1 20 0 20
x1 x1
x1
20 0 20
x1 x 1 0
x1
( )( ) 0 20
1 x 1 1 0
x1
20
1 1
x1
20
1 10
x1
0x 1 0 0x1 ()gx 0x1 0 x x 1 2
2
x1 1
x1
ln x0
23 个函数与导函数类型专题
第 2 页
故:
即:在 时, , 单调递减 ;
那么,在 时, 单调递 增 .
满足 ③ 式得 恰好是
⑷ 在 由 增 减 性 化 成 不 等 式
在 区 间 , 由 于 为单调递减函数,
故:
应 用 不 等 式 : 得:
即: , 即: 的 最 大 值 是
代入 ① 式 得 : ,即: , 即: ④
⑸ 在 由 增 减 性 化 成 不 等 式
在 区间, 由于 为单调递增函数,
故:
由于极限 , 故: , 代入 ① 式得: ⑤
⑹ 总 结 结 论
综合 ④ 和 ⑤ 式得: . 故: 的取值范围 是
本 题 的 要 点 : 求 出 的 最 小 值 或 最 小 极 限 值 .
特刊 : 数 值 解 析
由 ① 式 ,设函数
当 时 , 用 洛 必 达 法 则 得 : ln
2
2
x1 x0
x1
0 x x 1 '( )g x 0 ()gx 0 0xx ()gx 0x 0x1 ( , ) x1 ( , ) x1 ()hx ( ) lim ( )
x1
g x g x
ln lim 2 x1
2 x x
x1
23个函数与导函数类型专题.pdf